해시(Hash)
해시는 저장, 검색 등 자주 활용되는 자료구조이다. 또한 입력 데이터를 고정된 길이의 데이터로 변환한 값을 말한다.
데이터의 key값이 해시 함수를 통해 변환된 간단한 정수이며 정수로 변환된 해시는 배열의 인덱스, 위치, 데이터 값을 저장하거나 검색할 때 활용된다.
해시 함수 (Hash Function)
유일한 값(반복되지 않는 값)을 저장하기 위한 자료구조이며, Dictionary(Map) 자료구조와 같이 key, value 의 쌍 형태로 저장된다.
모든 데이터가 유일한 키값을 가져 해시 자료들은 특정한 값을 아주 빠르게 찾아낸다.
1. 직접 주소 테이블 (Direct Address Table)
유일한 키가 있다면 그냥 인덱스로 쓰면 되지 않을까? 즉, 입력받은 value가 곧 key가 되는 데이터 매핑 방식이다.
하지만 3개의 key값인 534, 644, 656이 있고 그대로 테이블에 넣어준다면 3개의 저장된 데이터를 제외하고 나머지는 undefined로 채워진다. 결국, 값은 없지만 메모리 공간은 할당되어 공간의 효율성이 좋지 못하게 된다.
공간의 효율성을 위해 인덱스를 매핑하는 '해시 함수'를 사용해 테이블을 만들고 그것을 '해시 테이블'이라고 한다.
2. 해시 테이블 (Hash Table)
해시 함수로 매핑된 최종 데이터이며 인덱스를 통해 액세스 할 수 있는 데이블에 (키, 값) 쌍을 저장하며 생성한다.
예시) 이메일 주소록을 저장해야하는 상황 (이름, 이메일)의 데이터
- (hayeon, hayeonn2@email.com)
- (hajun, hajunn2@email.com)
- (jungom, jungomm2@email.com)
이름을 key로 삼아 인덱싱 해야하며 앞서 말한 해시 함수를 이용하면 된다. 가장 흔한 형태의 해시 함수는 루즈 루즈(lose lose)함수 이다.
루즈 루즈 함수는 키를 구성하는 문자의 아스키 값을 단순히 더해 숫자로 리턴하는 함수이다.

1) 해시 테이블의 골격 만들기
function HashTable(){
const table = [];
}
2) 사용할 해시 함수 작성
// Lose Lose Hash Function
const hashFunction = (key) => {
let hash = 0;
for(let i = 0; i < key.length; i++){
hash += key.charCodeAt(i);
}
return hash;
}
key를 구성하는 문자 아스키 값을 합하는 함수이다. 결과 값을 저장할 변수 선언 후 key 문자열 길이만큼 반복해 문자별 아스키 값을 hash 변수에 더한다. 반복문이 종료되면 hash의 최종값을 반환한다.
3) 3가지 기본 메소드 추가하기
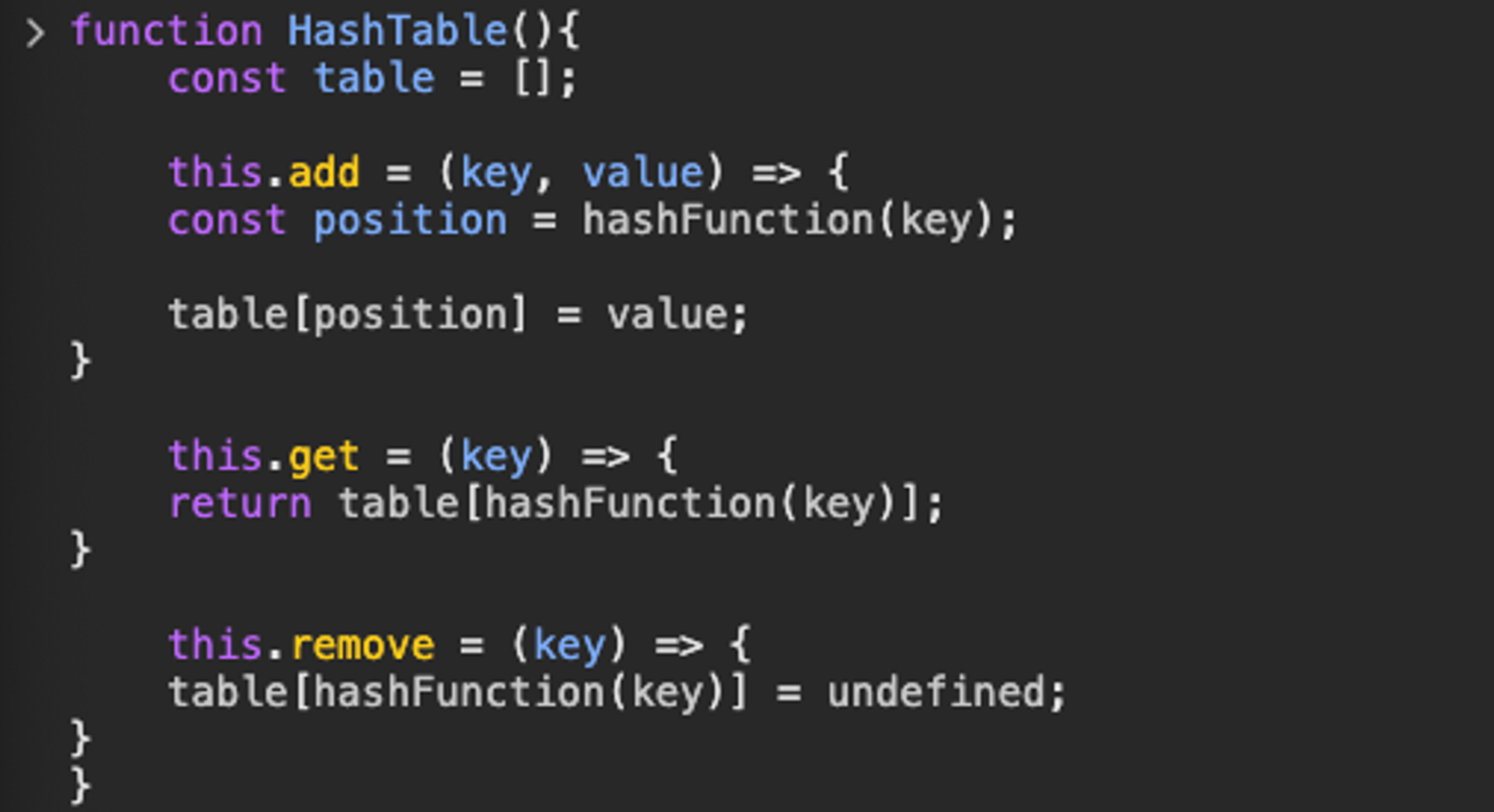
- add
this.add = (key, value) => {
const position = hashFunction(key);
table[position] = value;
}
key 인자를 해시 함수에 넣고 반환된 결과 값(position)으로 테이블에 저장해야 한다.
table 배열의 position 인덱스에 value를 추가한다.
- get : 데이터 읽어오기
this.get = (key) => {
return table[hashFunction(key)];
}
앞서 만든 해시 함수로 key의 인덱스 찾고, 인덱스에 해당하는 테이블 배열의 값 반환한다.
- remove : 데이터 삭제
this.remove = (key) => {
table[hashFunction(key)] = undefined;
}
해시테이블 인스턴스에서 원소를 삭제하려면 해시 함수를 이용해 인덱스를 찾아 테이블 배열의 값을 undefined로 만든다.
Array처럼 테이블 배열의 원소 자체를 삭제할 필요는 없다. 배열 전체에 원소들이 분포되어있어 어떤 인덱스엔 값이 할당되지 않은 채 기본 값 undefined 가 들어 있다.
4) Hash Table 클래스 사용하기
const hash = new HashTable();
hash.add("hayeon", "hayeonn2@email.com");
hash.add("hajun", "hajunn2@email.com");
hash.add("jungom", "jungomm2@email.com");
644 - hayeon
534 - hajun
656 - jungom
위와 같은 결과가 나오며, get 메소드도 잘 작동하는지 확인한다.
console.log(hash.get("hayeon")); // hayeonn2@email.com
console.log(hash.get("hajun")); // hajunn2@email.com
console.log(hash.get("SomeoneElse")); // undefined
“hayeon” 과 “hajun” 은 존재하는 key이므로 값을 반환하지만, “SomenoeElse”라는 key는 없으므로 배열에서 해시 함수에 의해 생성된 인덱스로 접근시 찾을 수 없으며 undefined를 반환한다.
이번엔 테이블에서 “hayeon”을 지워보자.

hash.remove("hayeon");
console.log(hash.get("hayeon"); // undefined
여기서 공간의 효율성을 좀 더 높여보자.
function hashFunction(key){
return key % 10;
}
해시 함수로 들어오는 key값을 10으로 나눈 후의 나머지를 반환한다. 어떤 값이 들어오든 그 값의 1의 자리만 반환한다. 그렇기 때문에 반환하는 값은 무조건 0 ~ 9 사이의 값이 나온다.
따라서 고정된 테이블의 길이를 정해둘 수 있고 그 안에만 데이터를 저장할 수 있다. 이로써 낭비되는 공간을 줄일 수 있게 된다.
해시의 충돌(Collision)
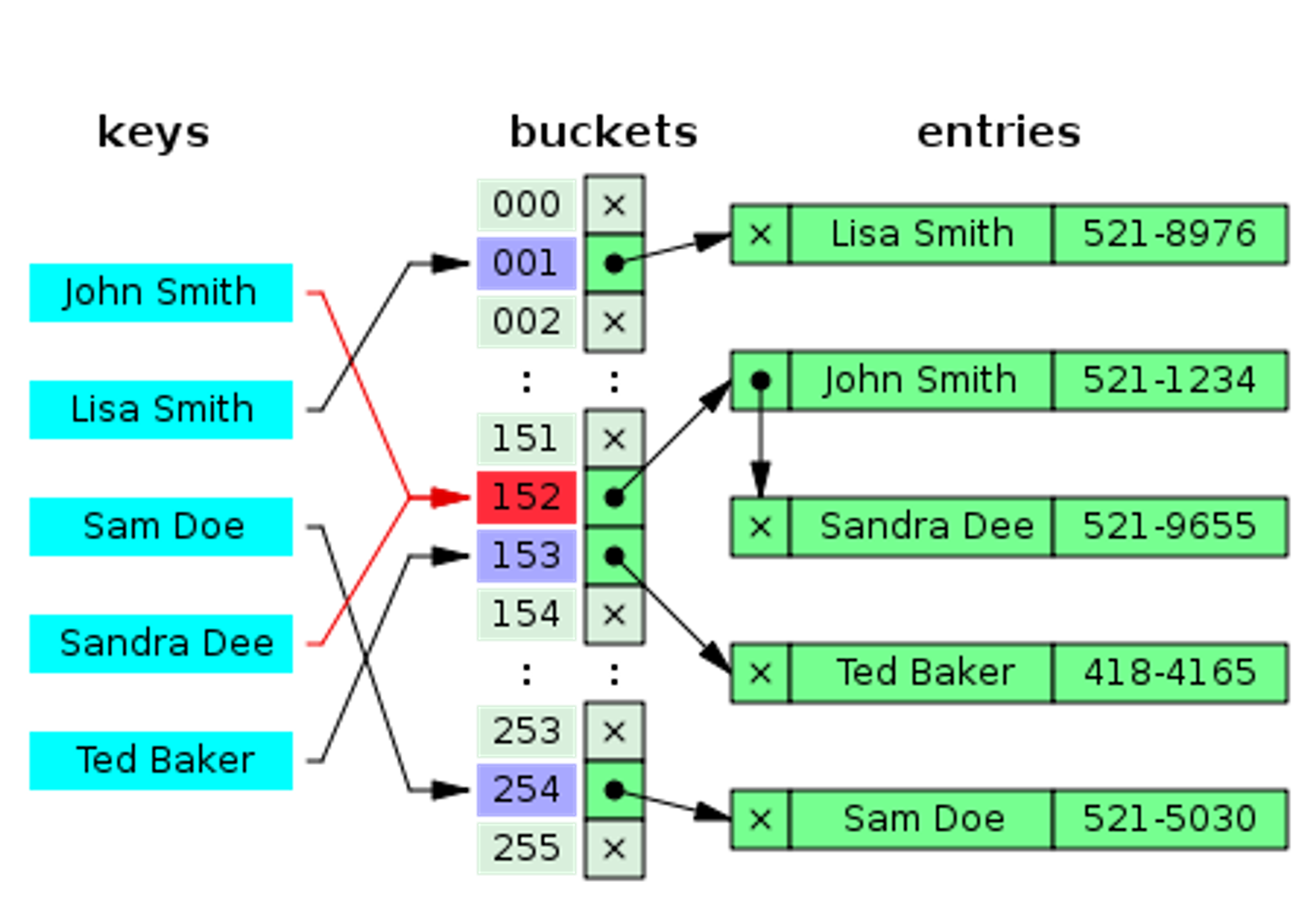
위의 그림과 같이 152라는 인덱스를 동일하게 배정받으면 어떻게 처리해야 할까?
개방 주소법 (Open Address)
충돌이 발생하면 테이블 내 새로운 주소를 탐사 후 비어있는 곳에 충돌된 데이터를 입력하는 방식이다.
해시 함수를 거쳐 나온 인덱스에 데이터가 이미 있으니, 다른 인덱스에 데이터를 저장한다는 의미로 개방 주소라고 부른다. 개방 주소법은 어떤 방식으로 비어있는 공간을 탐사할지에 따라 나눠진다.
1. 선형 탐사법 (Linear Probing)
선형 탐사법은 선형으로 순차적으로 탐사하는 방법이다.
function hashFunction(key){
return key % 10;
}
console.log(hashFunction(1001)); // 1
console.log(hashFunction(11)); // 1
1001의 해시 인덱스로 1이 나왔고 11 또한 1이 나온다. 이미 1번 인덱스에는 1001이 있기 때문에 11은 해시 테이블에 들어갈 자리가 없어진다. 이런 경우에 충돌이 일어났다고 말하며, 선형 탐사법은 충돌이 났을 때 정해진 칸 만큼의 옆 방을 주는 방법이다.

해시 함수에 key 값을 넣었을 때 또 1이 나온다면 충돌이 발생하며 값을 3번 인덱스에 저장한다. 이렇게 빈 공간이 나타날 때까지 순차적으로 탐사를 진행한다. 단점은 특정 해시 값의 주변이 모두 채워져 있는 일차 군집화 (Primary Clustering) 문제에 취약하다.
같은 해시가 여러번 나올 때, 선형 탐사법을 이용하면 데이터가 연속되게 저장 될 가능성이 높아진다. 이런 경우에 해시 값이 1이 나올 때 뿐만아니라 2, 3이 나왔을 때도 충돌이 발생한다. (이미 해시 값으로 2, 3에 해당하는 곳에 데이터가 저장되어 있어 계속해서 해시 값으로 1이 나오고 새롭게 2, 3이 나와도 저장하려는 공간에 데이터가 있어 계속 충돌하기 때문이다.)
이런식으로 충돌이 계속되면 데이터가 연속되게 저장돼 데이터 덩어리가 커진다. 이것이 일차 군집화이며 이러한 문제는 어떻게 해결할까?
2. 제곱 탐사법 (Quadratic Probing)
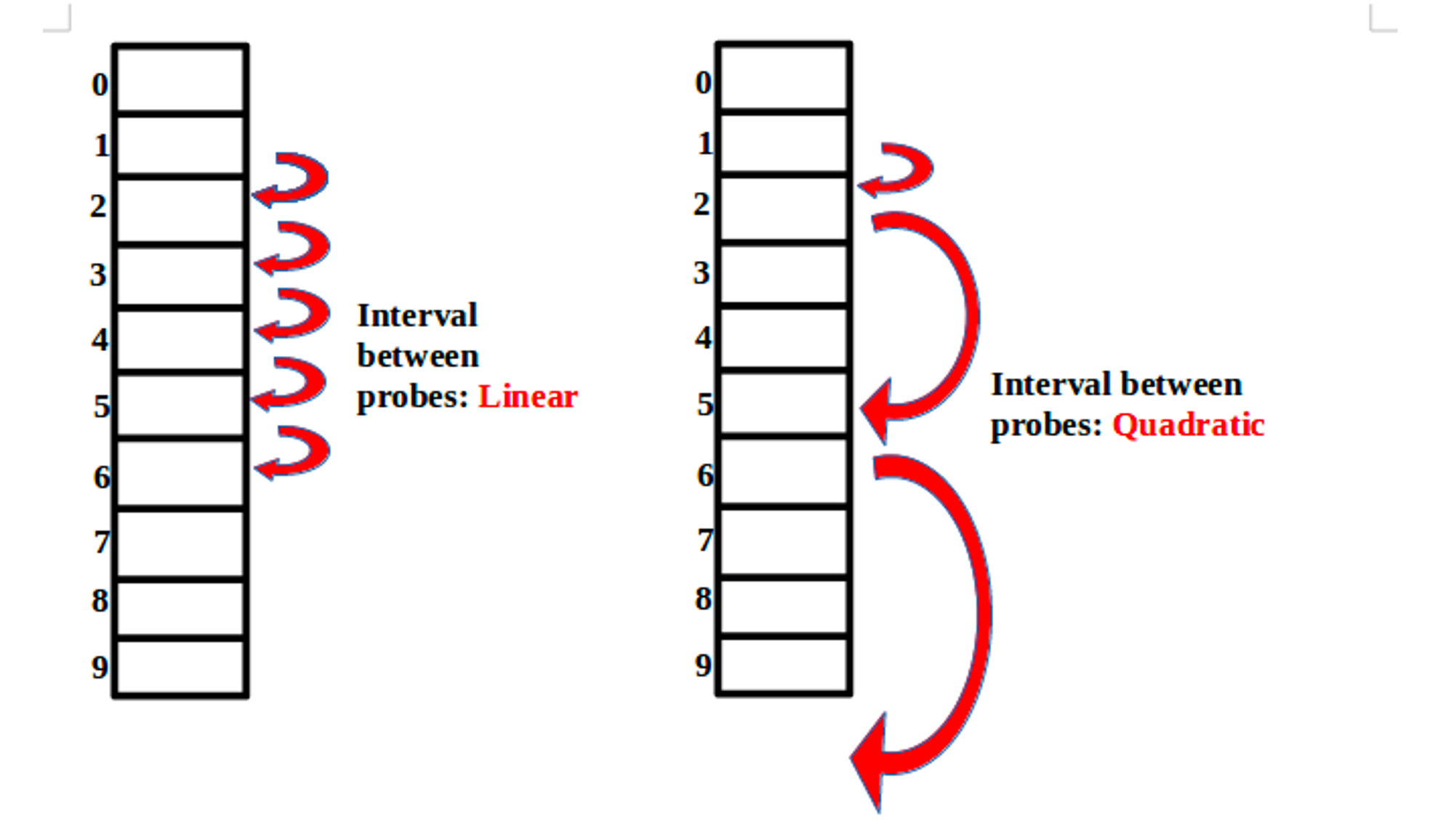
탐사하는 폭이 고정폭이 아닌 제곱으로 늘어난다. 1번째 충돌이 일어났을 때 충돌이 일어난 지점으로부터 1의 제곱만큼, 2번째 충돌이 일어났을 때 2의 제곱, 3번째는 3의 제곱... 이런식으로 탐사하는 스텝이 점점 커진다.
제곱 탐사법을 이용하면 충돌이 발생해도 데이터의 밀집도가 선형 탐사법보다 낮아 충돌 발생 확률이 낮다. 하지만 결국 해시로 1이 여러 번 나오면 계속 충돌이 일어나는건 마찬가지이다. 결국 데이터의 군집은 피할 수 없는 숙명이므로 이 현상을 이차 군집화(Secondary Clustering)이라고 부른다.
3. 이중 해싱 (Double Hashing)
함수를 이중으로 사용한다. 하나는 최초의 해시를 얻을 때 사용하고 두번 째는 충돌이 났을 때 탐사 이동폭을 얻기 위해 사용한다.
최초 해시로 같은 값이 나와도 다른 해시 함수를 거쳐 다른 탐사 이동폭을 제공해 다른 공간에 값이 골고루 저장될 확률이 높다.
const tableSize = 23; // 테이블 사이즈가 소수여야 효과가 좋다.
const hashTable = [];
const getSaveHash = (value) => value % tableSize;
// 스텝 해시에 사용되는 수는 테이블 사이즈보다 약간 작은 소수를 사용한다.
const getStepHash = (value) => 17 - (value % 17);
const setValue = (value) => {
// 1. 저장할 인덱스를 getSaveHash 해시 함수로 얻는다.
let index = getSaveHash(value);
// 2. index를 키로 받는 값을 targetValue 변수에 저장한다.
let targetValue = hashTable[index];
// 3. 반복문 시작
while(true){
// 4. targetValue가 없으면, 배열에 값이 비었다! -> 인덱스에 맞는 키값 저장
if(!targetValue){
hashTable[index] = value;
return;
}
// 5. 만약 배열의 길이가 테이블 사이즈보다 크거나 같으면 배열이 모두 꽉찼다.
else if (hashTable.length >= tableSize){
console.log("꽉 찼습니다.");
}
// 6. 인덱스 맞는 키값이 있고, 배열이 가득 차지 않았다면 인덱스에 맞는 키값을 저장하다가 충돌 발생
else {
console.log("충돌 발생");
index += getStepHash(value);
index = index > tableSize ? index - tableSize : index;
targetValue = hashTable[index];
}
}
}
테이블 사이즈와 두 번째 해시 함수에 사용되는 수는 소수를 사용하는 것이 좋다. 둘 중 하나가 소수가 아니라면 결국 언젠가 같은 해싱이 반복되기 대문이다.
console.log(setValue(1001)); // 12번
console.log(setValue(11)); // 11번
console.log(setValue(21)); // 21번
console.log(setValue(32)); // 9번
분리 연결법 (Separate Chaining)
분리 연결법은 해시 테이블의 버킷에 하나의 값이 아니라 링크드 리스트(Linked List)나 트리(Tree)를 사용한다.
링크드 리스트를 바탕으로 분리 연결법을 알아보자.
테이블 크기가 5일 때, 해시로 1을 반환하는 1001, 11, 21, 31을 저장한다. 이때 분리 연결법을 사용하면 이렇게 된다.

표를 보았을 때 [1001, 11, 21, 31] 의 순서가 아니라 [31, 21, 11, 1001]의 순서로 뒤집혀 있다. 이는 데이터를 삽입할 때 조금이라도 수행 시간을 줄이기 위해 사용하는 방법이다.
테이블 1번 인덱스에 저장된 링크드 리스트가 [1001, 11, 21, 31]의 순서일 때를 살펴보자.

다음 추가할 값이 41일 때, 메모리 주소가 99인 곳에 {값: 41, 다음 노드: null} 을 저장한다. 이 후 새로운 노드를 리스트에 붙여야하기 때문에 해당 리스트의 마지막 노드인 메모리 4에 저장된 값을 {값: 31, 다음 노드: 99}로 바꿔주면 된다.

이 때 새 노드를 리스트에 붙이기 위해 메모리 4에 저장된 노드를 찾는 과정이 문제가 된다.
먼저 리스트의 머리인 메모리 1부터 찾고 다음 메모리 주소 값을 확인하고 2로 이동해 또 다음 메모리 주소를 확인한다. 만약 이 리스트 길이가 계속 길어진다면 수행 시간도 비례해 늘어날 것이다. 하지만 순서를 반대로 뒤집으면 데이터 삽입이 쉬워진다.

맨 앞 노드를 추가하는 것이어서 다른 노드를 탐색할 필요없 이 메모리에 밀어 넣고 {값: 41, 다음노드: 1} 로 저장해주면 된다. 그래서 해시 테이블에 저장할 때 리스트의 꼬리에 데이터를 붙이기 보다 머리에 붙이는 방법을 보통 많이 사용한다.
이 때, 분리 연결법을 이용하려면 해시 함수의 역할이 아주 중요하다. 균일하지 못한 해시를 사용해 특정 인덱스에 데이터가 몰리게 된다면 다른 곳은 비어있지만 한 버킷에 저장된 리스트의 길이만 계속 길어질 것이다.
결국, 내가 찾고자 하는 값이 리스트의 맨 마지막에 위치한다면 링크드 리스트를 처음부터 끝까지 탐색해야하므로 O(n)의 시간 복잡도를 가지게 된다. 때문에 최대한 저장하고자 하는 데이터를 균일히게 퍼트려 리스트의 길이를 어느 정도로 유지해주는 해시 함수의 역할이 중요하다.
그림으로 보는 예시
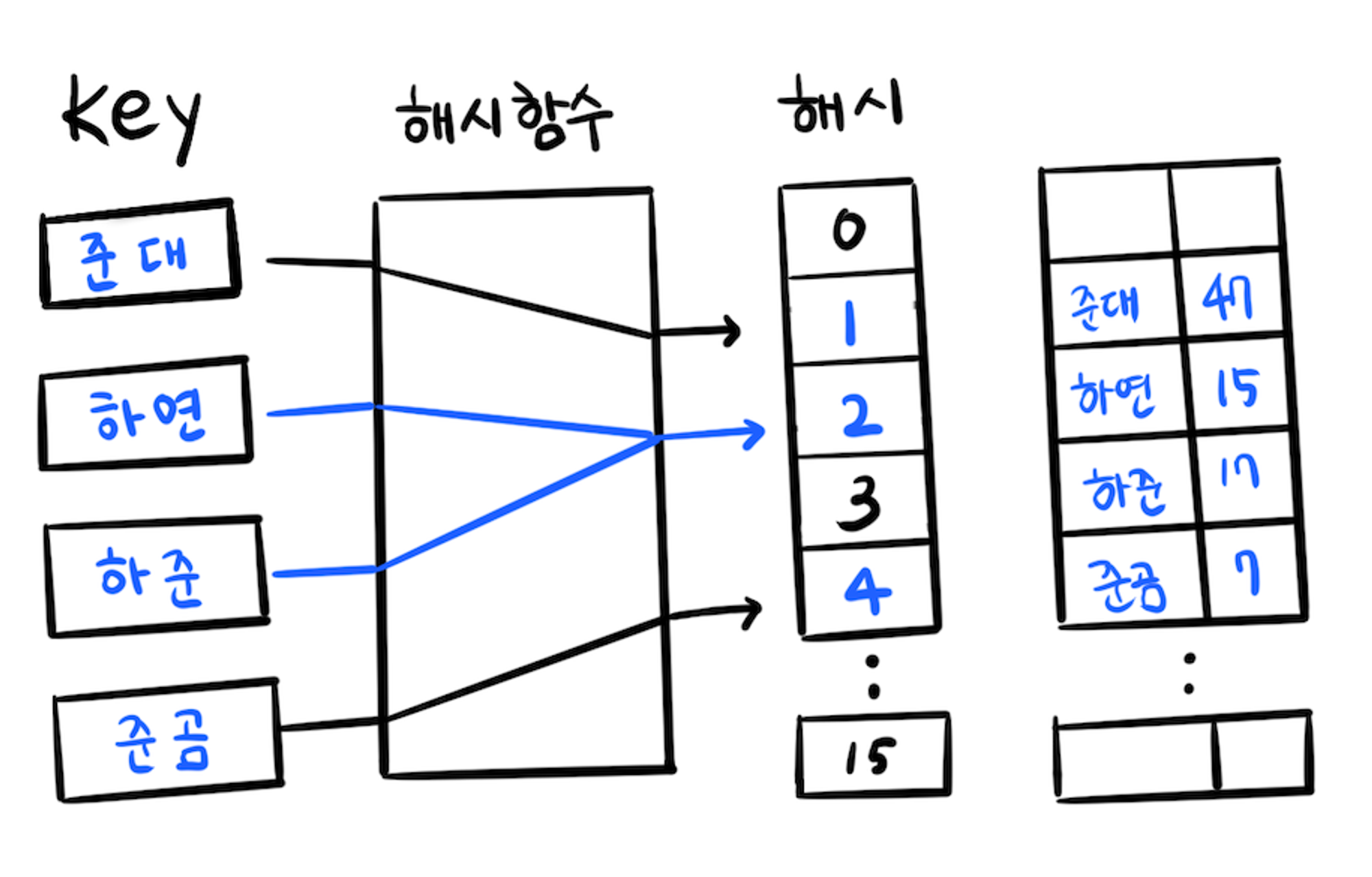
1. 개방 주소법을 사용해 데이터를 저장하기
같은 인덱스 값을 받아 충돌이 일어나며 하연을 인덱스 2에 저장하면 하준은 인덱스 2에 값을 저장하지 못해 빈 공간을 찾아 값을 저장한다. 군집화의 문제가 발생할 수 있어 단점이 있다.
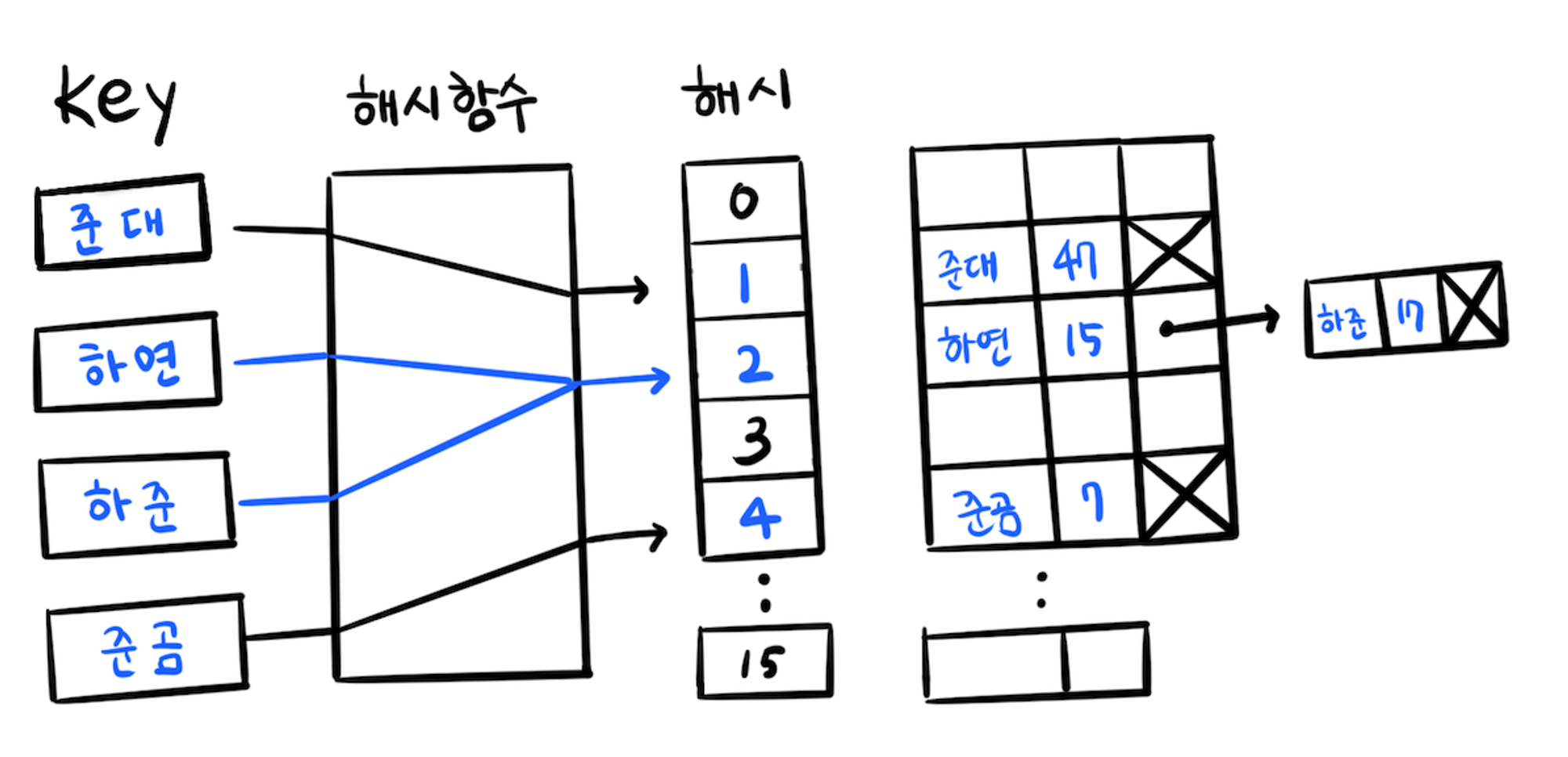
2. 분리 연결법을 사용해 데이터 저장하기
하연과 하준은 해시 함수를 거치며 같은 인덱스 값을 받아 충돌이 난다. 하연을 인덱스 2에 저장한다면 개방 주소법의 경우 빈 공간에 데이터를 저장하지만 분리 연결법은 링크드 리스트를 활용해 같은 인덱스에 값을 저장하며 테이블을 형성한다. 예시에서 하준을 꼬리에 저장했지만 좀 더 효율적으로 데이터를 쌓으려면 머리 쪽에 데이터를 쌓으면 된다.
테이블 크기 재할당 (Resizing)
해시 테이블은 고정적인 공간을 할당해 많은 데이터를 담기 위한 자료구조여서 언젠가 데이터가 넘친다. 개방 주소법을 사용한다면 테이블이 실제로 꽉 차 더 이상 저장을 못하는 상황이 생기게 된다. 분리 연결법을 사용하는 경우 충돌이 발생할수록 각각의 버킷에 저장된 리스트가 점점 더 길어져 리스트를 탐색하는 리소스가 너무 늘어나게 된다.
따라서, 해시 테이블은 어느정도 비워져 있는 것이 성능상 좋다. 해시 테이블을 운용할 때 어느 정도 데이터가 차면 테이블의 크기를 늘려줘야 한다. 특별한 알고리즘없이 기존 크기의 2배 정도 새로운 테이블을 선언해 기존 테이블의 데이터를 그대로 옮겨 담는다.
분리 연결법을 사용한 해시 테이블 경우 재 해싱을 통해 너무 길어진 리스트의 길이를 나눠 다시 저장하는 방법을 사용하기도 한다.
테이블의 크기는 언제 늘려야 할까? 대개 사용률이 0.7 이상으로 커지면 해시 테이블을 리사이징 하며 대략 2배 정도의 크기로 배열을 만든다.
- 사용률 계산하기 : 해시 테이블에 저장된 항목 수 / 해시 테이블 공간 수
위와 같이 구할 수 있으며 만약 테이블에 5개의 버킷이 있고 그 중 2개의 버킷에 데이터가 저장되어 있다면 2/5 = 0.4 의 사용률을 구할 수 있다. 저장할 데이터가 100개일 때, 개방 주소법을 사용해 생각한다면 해시 테이블에 최소 100개의 공간이 있어야 하고 만약 100개의 데이터에 100개의 버킷이 있다면 해시 테이블의 사용률은 1이 된다. 이런식으로 계산해 사용률이 0.7 이상이 되면 해시 테이블을 리사이징 해준다. 리사이징을 해 배열을 크게 만들고 나면 해시 함수를 사용해 기존 테이블에 있던 데이터를 새로운 해시 테이블에 다시 저장해야 한다. 이러한 과정은 시간이 매우 오래 걸리므로 자주 하는 것은 좋지 않다.
자바스크립트에서 해시 테이블
해시맵을 활용해 다양한 배열 요소를 만들 수 있다. 이중 배열도 가능하며 여러 키와 값을 가진 배열도 만들 수 있다. JS에서 해시테이블은 대표적으로 Object, Map, Set이 있다. JS에서 key-value로 이루어진 자료구조는 Object가 대표적이었지만 ES6에서 Map, Set이 추가되었다.
Map 객체란?
- 주로 Object와 비교됨
- key-value로 이루어진 해시 테이블
- 탐색은 get(), 삽입은 set()으로 한다.
- key는 고유값이며 단 1개만 존재한다.
- key 가능 자료형 : number, string, function, object, NaN
Map의 메소드
1) value 설정 : set()
const map = new Map();
let number = 0;
let str = 'str';
let obj = {a: 1};
let fnc = () => {
console.log('fnc');
};
map.set(number, 4)
map.set(str, 1)
map.set(obj, 2)
map.set(fnc, 3)
map.set(number, 0)
console.log(map);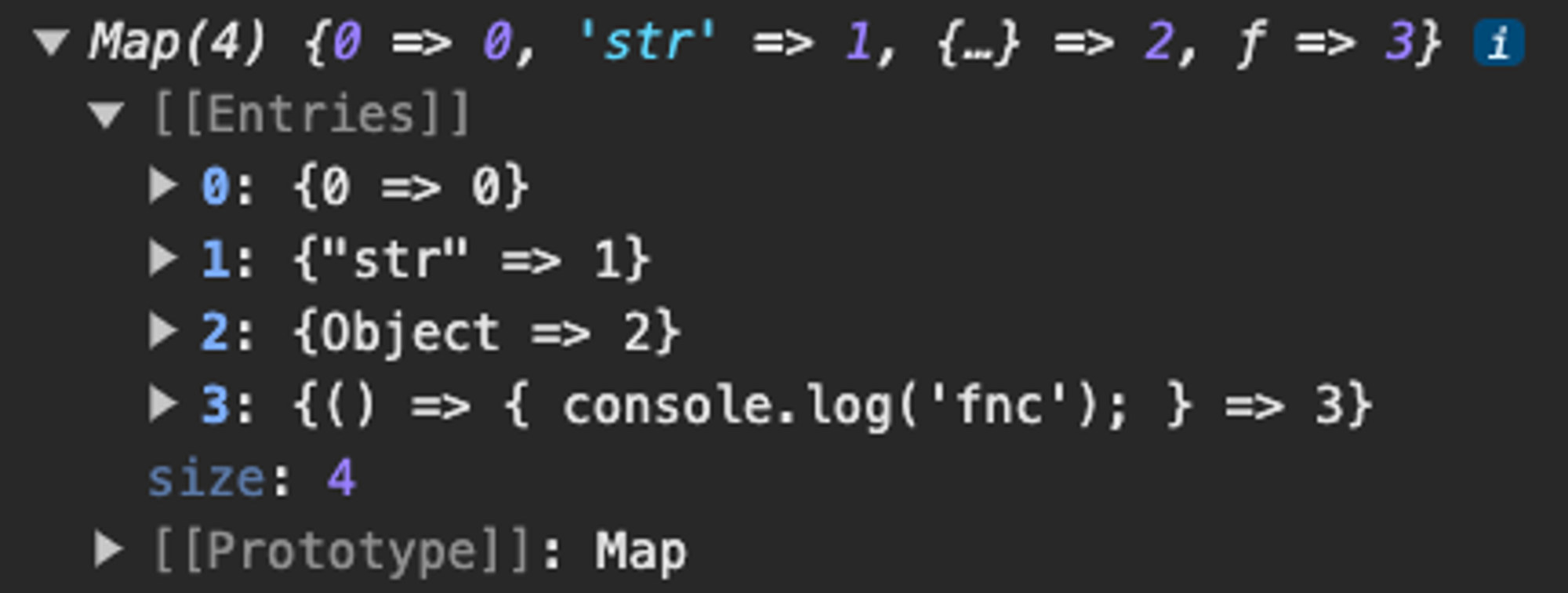
2) value 얻기 : get()
// 위의 코드 사용
map.get(str); // 1
map.get(obj); // 2
map.get('none'); // undefined
map.get({ a: 1 }); // undefined, obj !== { a: 1 }
3) value 찾기 : has()
// 위 코드 재사용
map.has(str); // true
map.has(obj); // true
map.has('none'); // false
4) value 삭제 : delete()
// 코드 재사용
map.delete(str); // true
map.delete('none'); // false
5) value 존재 유무 : size
map.size // 4
map.length // undefined
6) hash 탐색 : for-of 문
// key, value 쌍으로 출력
for(let [key, value] of map){
console.log(key + '-' + value);
}
// key 출력
for(let key of map.keys()){
console.log(key);
}
// value 출력
for(let value of map.values()){
console.log(value);
}
해시 테이블의 장단점
장점
- 중복 데이터를 찾아내기 쉽다.
- 빠르게 데이터 탐색, 삽입, 삭제 가능
단점
- 공간 효율성이 낮다.
- 직접 주소 테이블보다 좋다고 할 수 있지만 해시 테이블도 미리 빈 공간을 만들어 데이터를 넣는 방식이라 만들어둔 공간에 데이터가 들어가지 않는다면 공간 효율성이 좋지 못한 사례가 될 수 있다.
- 정렬된 데이터를 다루기 적절하지 않아 해시 함수에 대한 의존도가 매우 높다.
- 만약 해시 함수의 성능이 나쁘거나 함수가 원하는대로 작동하지 않는다면 해시 테이블의 성능, 효율도 나빠진다.
해시 테이블의 Big-O (시간 복잡도)
충돌이 발생할 경우와 발생하지 않은 경우가 있다.
검색 단계
충돌이 발생하지 않은 경우 검색 단계의 시간 복잡도는 O(1)이다. 키는 고유하고 해시 함수의 결과로 나온 해시에 매칭되는 값을 찾으면 되기 때문이다. 해시 함수의 시간 복잡도는 함께 고려하지 않지만 최악의 경우 O(n)이 될 수 있다. 해시 충돌로 인해 모든 버킷의 값들을 찾아봐야할 때가 있다.
저장 단계
충돌이 발생하지 않은 경우 시간 복잡도는 O(1)이다. 키는 고유하며 해시함수의 결과로 나온 해시, 값을 저장소에 넣으면 되기 때문이다. 이때 해시함수의 시간 복잡도는 함께 고려하지 않지만 최악의 경우 O(n)이 될 수 있다. 해시 충돌로 인해 모든 버킷의 값들을 찾아봐야할 때가 있다
삭제 단계
충돌이 발생하지 않은 경우 시간복잡도는 O(1)이다. 저장되어 있는 값을 삭제할 때 저장소에서 해당 키와 매칭되는 값을 찾아 삭제하면 된다. 이때 해시함수의 시간 복잡도는 함께 고려하지 않지만 최악의 경우 O(n)이 될 수 있다. 해시 충돌로 인해 모든 버킷의 값들을 찾아봐야할 때가 있다.
충돌을 방지하는 방법들은 데이터의 규칙성(클러스터링)을 방지하기 위한 방식이지만 공간을 많이 사용한다는 단점이 있다. 만약 테이블이 꽉 차있다면 테이블을 확장해야하는데 이것은 심각한 성능 저하를 불러오기 때문에 가급적이면 확장을 하지 않도록 테이블을 설계해야 한다. 또한, 해시 테이블에서 자주 사용하게 되는 데이터를 캐시에 적용하면 효율을 높일 수 있다. 자주 hit 하게 되는 데이터를 캐시에서 바로 찾아 해시 테이블의 성능을 향상시킬 수 있다.
'개발' 카테고리의 다른 글
| [React/CRA] CRA + typescript + Eslint + prettier 초기 세팅하기 (1) | 2024.01.23 |
|---|---|
| [성능 최적화] 웹 성능 최적화에 대한 고찰과 최적화 하는 방법을 알아보자 (3) | 2024.01.18 |
| [자료구조] 이분 탐색/이진 탐색 (Binary Search) (1) | 2024.01.04 |
| CSRF(Cross Site Request Forgery)와 XSS(Cross Site Scripting) (0) | 2023.12.02 |
| [Webpack5 + typescript] resolve alias 절대경로 설정하기 (0) | 2023.08.28 |
